В евклидовой геометрии сумма внутренних углов любого треугольника всегда равна 180°. Рассмотрим несколько способов доказательства этого фундаментального свойства.
Содержание
Классическое доказательство через параллельные прямые
- Пусть дан треугольник ABC
- Проведем через вершину B прямую DE, параллельную стороне AC
- Угол DBA равен углу BAC как накрест лежащие
- Угол EBC равен углу BCA как накрест лежащие
- Углы DBA, ABC и EBC образуют развернутый угол, равный 180°
- Следовательно, ∠A + ∠B + ∠C = 180°
Графическая иллюстрация доказательства
| Шаг | Описание |
| 1 | Исходный треугольник ABC |
| 2 | Проведение параллельной прямой DE через вершину B |
| 3-4 | Образование равных углов при параллельных |
| 5-6 | Суммирование углов в развернутом угле |
Доказательство через свойства многоугольников
- Сумма внутренних углов n-угольника равна (n-2) × 180°
- Для треугольника (n=3): (3-2) × 180° = 180°
- Это следует из разбиения многоугольника на треугольники
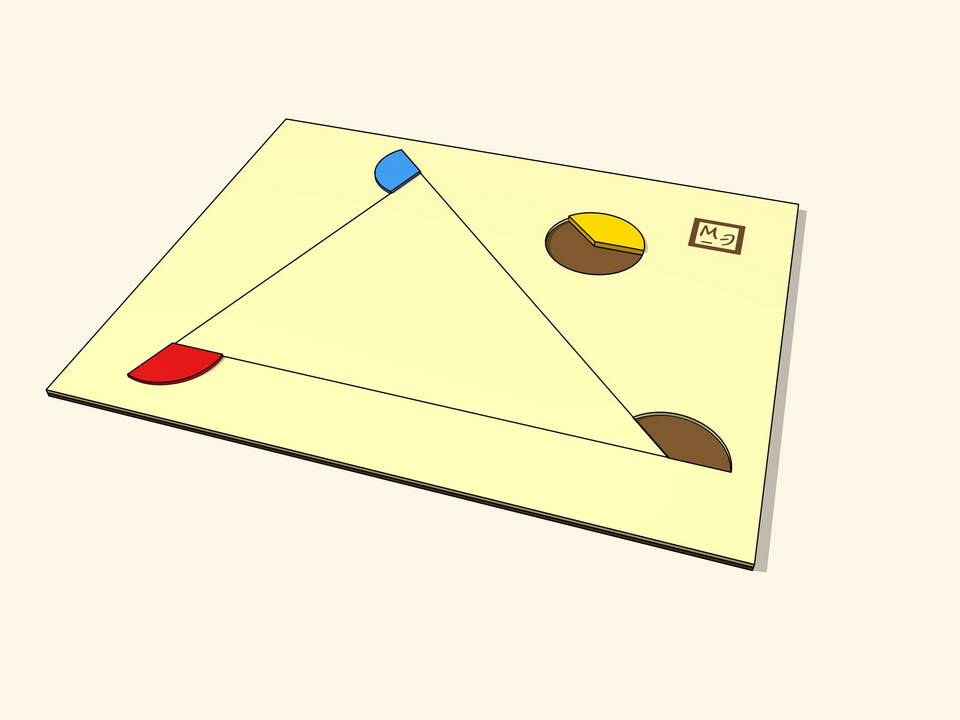
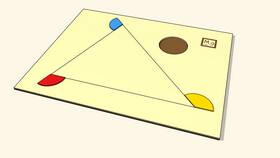
Экспериментальное доказательство
Практический способ подтверждения теоремы:
- Нарисуйте любой треугольник на бумаге
- Аккуратно отрежьте его углы
- Сложите отрезанные углы вершинами вместе
- Убедитесь, что они образуют развернутый угол (180°)
Доказательство в неевклидовых геометриях
| Тип геометрии | Сумма углов треугольника |
| Евклидова | Ровно 180° |
| Сферическая | Более 180° |
| Гиперболическая | Менее 180° |
Историческая справка
Доказательство суммы углов треугольника известно со времен древнегреческих математиков. Евклид включил это положение как 32-е предложение в первую книгу своих "Начал". Это свойство лежит в основе многих геометрических теорем и построений.
Применение теоремы на практике
- Расчет неизвестных углов в геометрических задачах
- Проверка правильности построения треугольников
- Основы тригонометрических вычислений
- При проектировании в архитектуре и инженерии
Заключение
Доказательство суммы углов треугольника является краеугольным камнем евклидовой геометрии. Различные методы доказательства - от классических до экспериментальных - подтверждают это фундаментальное свойство, которое находит широкое применение в математике и ее приложениях.