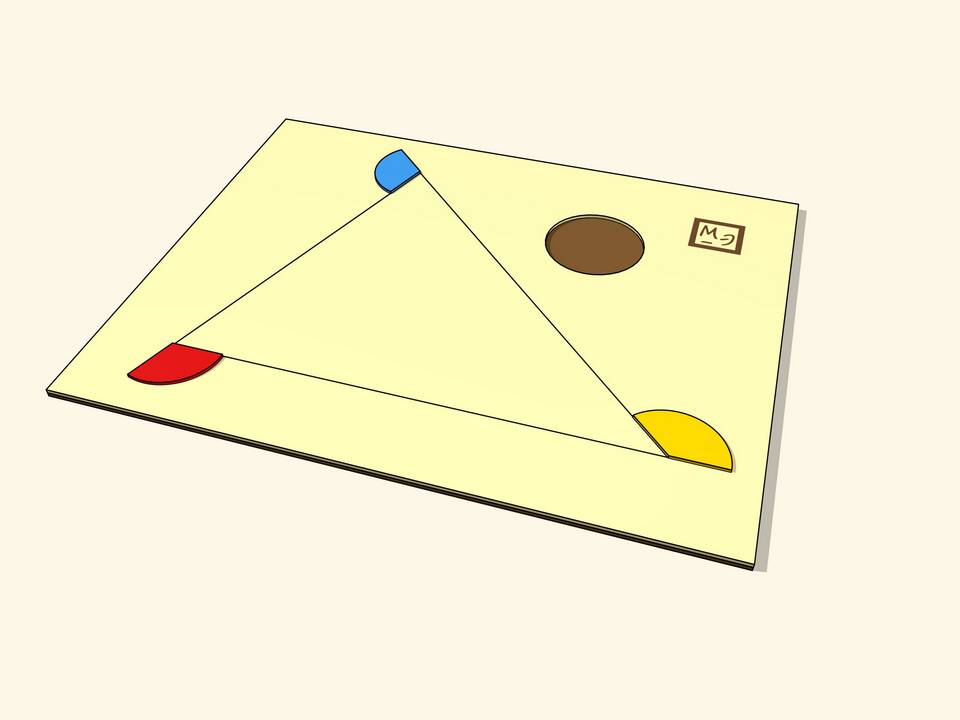
Внешним углом треугольника называется угол, смежный с внутренним углом треугольника. При каждой вершине треугольника можно построить два равных внешних угла, расположенных по разные стороны от продолжения стороны.
Содержание
Определение внешнего угла треугольника
Теорема о сумме внешних углов
Сумма внешних углов треугольника, взятых по одному при каждой вершине, равна 360°.
Доказательство теоремы
- Рассмотрим произвольный треугольник ABC
- Обозначим его внутренние углы как α, β, γ
- По теореме о сумме внутренних углов треугольника: α + β + γ = 180°
- Построим внешние углы при каждой вершине:
- Внешний угол при вершине A = 180° - α
- Внешний угол при вершине B = 180° - β
- Внешний угол при вершине C = 180° - γ
- Найдем сумму внешних углов:
(180° - α) + (180° - β) + (180° - γ) = 540° - (α + β + γ)
- Подставим сумму внутренних углов:
540° - 180° = 360°
Графическое представление
| Вершина | Внутренний угол | Внешний угол |
| A | α | 180° - α |
| B | β | 180° - β |
| C | γ | 180° - γ |
| Сумма внутренних углов | 180° | |
| Сумма внешних углов | 360° | |
Альтернативное доказательство
Рассмотрим движение вокруг треугольника:
- Совершая полный оборот вокруг треугольника, мы поворачиваемся на 360°
- Этот поворот складывается из поворотов на внешние углы
- Следовательно, сумма внешних углов равна полному обороту - 360°
Вывод
Представленные доказательства подтверждают, что сумма внешних углов треугольника, взятых по одному при каждой вершине, всегда равна 360°, независимо от вида треугольника (остроугольный, прямоугольный, тупоугольный).