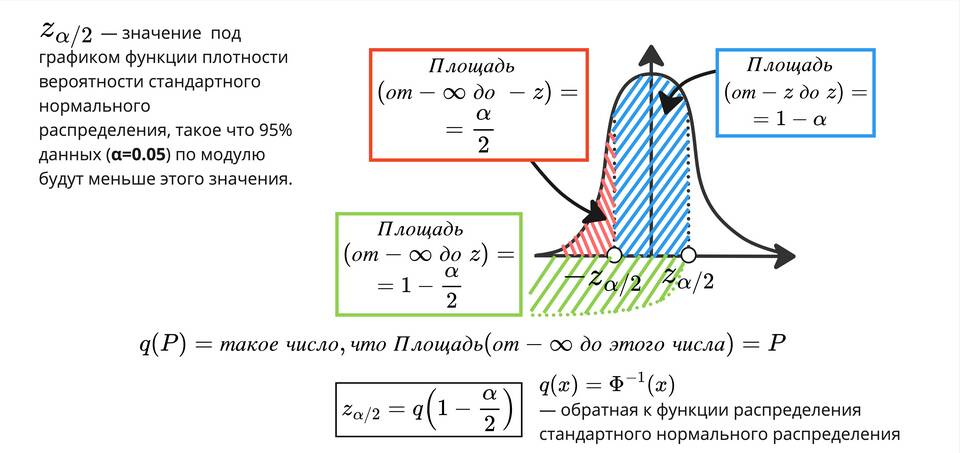
Доверительный интервал - это диапазон значений, который с определенной вероятностью содержит истинное значение оцениваемого параметра. Рассмотрим методику его расчета для различных статистических задач.
Содержание
Доверительный интервал - это диапазон значений, который с определенной вероятностью содержит истинное значение оцениваемого параметра. Рассмотрим методику его расчета для различных статистических задач.
1. Основные понятия
| Термин | Определение |
| Доверительный уровень | Вероятность, с которой интервал содержит параметр (обычно 90%, 95% или 99%) |
| Точечная оценка | Выборочное значение оцениваемого параметра |
| Предельная ошибка | Половина ширины доверительного интервала |
2. Расчет для среднего значения (нормальное распределение)
2.1. При известном σ
Формула: CI = x̄ ± z*(σ/√n)
- Вычислите выборочное среднее (x̄)
- Определите z-критическое значение для выбранного уровня доверия
- Рассчитайте стандартную ошибку (σ/√n)
- Умножьте z-значение на стандартную ошибку
3. Расчет для доли признака
| Условие | Формула |
| Большая выборка (np>10, n(1-p)>10) | p̂ ± z*√(p̂(1-p̂)/n) |
| Малая выборка | Использовать точные методы (Клоппера-Пирсона) |
4. Расчет для малых выборок
- Используйте t-распределение вместо нормального
- Формула: x̄ ± t*(s/√n)
- Степени свободы: n-1
- t-критическое значение зависит от объема выборки
5. Пошаговый алгоритм расчета
- Определите параметр для оценки (среднее, доля, разница)
- Выберите доверительный уровень (обычно 95%)
- Рассчитайте точечную оценку параметра
- Определите стандартную ошибку оценки
- Найдите критическое значение распределения
- Вычислите предельную ошибку
- Постройте интервал: оценка ± ошибка
6. Пример расчета для среднего
| Параметр | Значение |
| Выборочное среднее (x̄) | 50 |
| Стандартное отклонение (s) | 10 |
| Объем выборки (n) | 30 |
| 95% ДИ | 50 ± 2.045*(10/√30) = [46.27; 53.73] |
Заключение
Определение доверительного интервала требует понимания типа распределения, объема выборки и характера оцениваемого параметра. Правильно рассчитанный доверительный интервал позволяет сделать обоснованные выводы о генеральной совокупности на основе выборочных данных.
